Break-Even-Analyse

Inhaltsverzeichnis
Definition: Break-Even-Analyse
Der Break-Even-Point, auch Break-Even-Analyse genannt, ist der Punkt einer Produktion, bei dem Kosten und Erlös eines Punktes identisch sind. Es ergibt sich also weder ein Gewinn noch ein Verlust. Deutsche Bezeichnungen für diesen Punkt sind Gewinnschwelle oder Nutzenschwelle. Die Ermittlung dieses Punktes wird als Break-Even-Analyse bezeichnet. Kann ein Unternehmen die Produktionskosten senken oder den Erlös steigern, erzielt es Gewinne.
Formel: [1] E = Kge
oder
[2] p x = Kf + kv x
Berechnung des Break-Even-Points
Mithilfe von Gleichungen kann die Nutzenschwelle für ein Produkt bzw. mehrere Produkte berechnet werden.
Daraus ergibt sich als Deckungsausbringung (kritische Stückzahl):
[3] xkrit = Kf/p – kv oder krit = Kf / db
E = Erlös, Umsatz
Kges = Gesamtkosten
p = Verkaufspreis
x = Stückzahl, Verkaufsmenge
kv = variable Stückkosten
Kf = Fixkosten, Strukturkosten
db = Stückdeckungsbeitrag
Die Nutzenschwelle ist also dann erreicht, wenn Umsatz- und Kostenvolumen identisch sind. Durch die Umformung der Gleichungen können verschiedenen Fragestellungen der Break-Even-Analyse beantwortet werden.
Einsatzgebiete der Break-Even-Analyse
Die Break-Even-Analyse wird in Unternehmen genutzt, um betriebswirtschaftliche Überlegungen, die mit Umsatz- und Kostenstrukturen zusammenhängen, anzustellen. Sie kann angewendet werden, um den aktuellen Stand der Dinge zu analysieren oder bei Entscheidungen für die Zukunft zu unterstützen, zum Beispiel in Bezug auf Investitionen oder zusätzliche Mitarbeiter.
Achtung
Obwohl die Break-Even-Analyse in jedem Unternehmen zum Einsatz kommen kann, muss sich doch mit Vorsicht angewandt werden. Sie ist nur dann aussagekräftig, wenn Kosten und Erlöse einzelnen Produkten, Produktgruppen oder Bereichen korrekt zugeordnet werden.
Welche Daten werden für die Berechnung des Break-Even-Points benötigt?
Für die Berechnung der Nutzenschwelle werden verschiedene Informationen benötigt, unter anderem:
- Stückpreis für ein Produkt
- Nettoverkaufspreis
- Jährliches (bzw. monatliches) Fixkostenvolumen
- Menge der verkauften Produkte
- Variable Kosten für ein Produkt
Der Break-Even-Point ist genau der Punkt, an dem der Gewinn gleich Null ist.
Die Break-Even-Analyse in der Praxis
Grundgleichung [2] gilt stets als Ausgangspunkt für alle Fragestellungen:
p x = Kf + kv x
Den darin enthaltenen Zusammenhang verdeutlicht zeigt Abb. 1:

Abb. 1: Grafische Darstellung mit Umsatz- und Gesamtkostenverlauf
In der grafischen Darstellung entspricht der Anstiegswinkel der Gesamtkostenkurve den variablen Stückkosten. Der Anstiegswinkel der Umsatzkurve entspricht dem Stückerlös. Ein Umsatzvolumen unterhalb des Deckungspunktes führt zu einem Verlust, ein Umsatzvolumen größer als der Deckungspunkt bedeutet Gewinn.
Für viele Fragestellungen ist die Darstellung des Zusammenhangs mit Abb. 2 zweckmäßig.
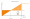
Abb. 2: Grafische Darstellung von Gewinn oder Verlust ja nach Ausbringung
Der Deckungspunkt ist dort erreicht, wo die Deckungsbeitragskurve die Kurve des Fixkostenblocks schneidet. Jede verkaufte Leistungseinheit oberhalb des Deckungspunktes steigert den Gewinn in Höhe des Stückdeckungsbeitrags. Unterhalb des Deckungspunktes entsteht mit jeder weniger abgesetzten Leistungseinheit ein Verlust in Höhe des Stückdeckungsbeitrags.
Mit Gleichung [3] wird die Frage nach der kritischen Absatzmenge beantwortet. Der Deckungsumsatz kann daraus wie folgt abgeleitet werden

Der im Nenner der Gleichung [3] stehende Ausdruck lässt sich auch umformen in

Diese Relation (Deckungsbeitrag zu Preis) bezeichnet man auch als Deckungsgrad, sodass [3] auch geschrieben werden kann als:

Soll die Frage beantwortet werden, in welcher Weise das Absatzpreisniveau verändert werden kann, um bei sonst gleichbleibenden Daten Kostendeckung zu erzielen, so ist Ausgangsgleichung [2] nach der kritischen Größe p aufzulösen:

Soll ermittelt werden, in welchem Umfang die variablen Stückkosten ansteigen können, ohne dass das Unternehmen in die Verlustzone abgleitet, ist die Ausgangsgleichung [2] nach der kritischen Größe kv aufzulösen:
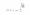
In gleicher Weise kann das kritische Fixkostenvolumen bestimmt werden:
[8] Kf krit = x db
Interessant für die Beurteilung des Verlustrisikos ist die Ermittlung der Sicherheitsspanne. Diese gibt an, wie groß die Differenz zwischen geplanter Absatzmenge xP und Deckungsmenge ist.

Bei den bisherigen Überlegungen wurde der Break-even entweder für das Gesamtunternehmen bestimmt oder für eine Produktart/Produktgruppe isoliert betrachtet.
Im Mehrproduktfall ist die Break-even-Analyse mehrdeutig. Es gibt viele Absatzmengenkombinationen der einzelnen Erzeugnisse, die alle zur Kostendeckung führen. Um eine Deckungsanalyse durchführen zu können, geht man von einer konstanten Zusammensetzung des Umsatzes im Hinblick auf den Anteil der einzelnen Produktarten aus. Es wird unterstellt, dass sich die in der Absatzplanung zugrunde gelegte Zusammensetzung des Sortiments im Ist im gleichen Mix realisiert.
Der Deckungsumsatz im Mehrproduktfall errechnet sich als:

So gehen Sie bei der Anwendung der Break-even-Analyse vor
Die Vorgehensweise soll für verschiedene Fragestellungen anhand eines Beispiels erläutert werden.
Praxis-Beispiel
Beispiel einer Break-even-Analyse
Ein Unternehmen hat sich auf eine Serienproduktion und den Absatz eines Spezialprodukts spezialisiert. Die Planung für das Jahr 01 legt folgende Daten zugrunde:
Verkaufspreis: | 258 | EUR/Stück |
|---|---|---|
Stückkosten: | 207 | EUR |
Fixkosten: | 1.268.000 | EUR/Jahr |
variable Stückkosten: | 162 | EUR/Stück |
geplante Absatzmenge im Jahr: | 22.000 | Stück |
Fertigungszeit: | 19,4 | Min./Stück |
Kapazität bei Normalarbeitszeit: | 600 | Std./Monat |
Welcher Anstieg der variablen Kosten, z. B. aus der Lohnerhöhung oder Materialpreiserhöhung, kann verkraftet werden, ohne dass Verluste entstehen?
Ermittlung nach Formel [7]
200,36 EUR/Stück
Anstieg um 23,7%
Fragen: | Ergebnis: |
|---|---|
Bei welcher Absatzmenge ist die Kostendeckung erreicht? | 13.208 Stück |
Bei welchem Umsatz ist die Kostendeckung erreicht? | 3.407.750 EUR |
Bei welcher Kapazitätsauslastung ist die Kostendeckung erreicht? | 59,3% Beschäftigungsgrad |
Wie groß ist die Sicherheitsspanne? | 40% |
Wie groß ist der Gewinn bei Erzielung der Planabsatzmenge? | 844.000 EUR |
Welche Preisreduzierung kann verkraftet werden, ohne dass Verluste entstehen? | 219,63 EUR/Stück |
Welcher Anstieg der variablen Kosten, z. B. aus der Lohnerhöhung oder Materialpreiserhöhung, kann verkraftet werden, ohne dass Verluste entstehen? | 200,36 EUR/Stück |
Welcher Anstieg des Fixkostenblocks, z. B. aus Erhöhung Miete, Gehaltssteigerungen etc., kann verkraftet werden, ohne dass Verluste entstehen? | 2.112.000 EUR |
Praxis-Beispiel
Beispiel einer Break-even-Analyse
Ein Softwarehaus und Beratungsunternehmen plant für das Jahr 01 den Absatz folgender Leistungen:
Umsatz | Leistungskosten | |
|---|---|---|
Softwareprodukt A | 2,80 Mio EUR | 260 TEUR |
Softwareprodukt B | 1,70 Mio EUR | 178 TEUR |
Einführungsunterstützung | 1,350 Mio EUR | 990 TEUR |
Programmierung | 1,480 Mio EUR | 1.200 TEUR |
im Kundenauftrag | 1,160 Mio EUR | 945 TEUR |
Wartungsleistungen | 0,420 Mio EUR | 410 TEUR |
Schulungsleistungen | ||
Bereitschaftskosten | 4,265 Mio EUR | |
Frage: Welcher Umsatz führt zum Break-even? |
Deckungsumsatz und Sicherheitsspanne
| Umsatz | Leistungs- kosten | DB | Deckungs- grad | Rang | ||
| TEUR | TEUR | TEUR | ||||
| Softwareprodukt A | 2.800 | 260 | 2.540 | 0,9071 | 1 | |
| Softwareprodukt B | 1.700 | 178 | 1.522 | 0,8953 | 2 | |
| Einführungsunterstützung | 1.350 | 990 | 360 | 0,2667 | 3 | |
| Programmierung im Kundenauftrag | 1.480 | 1.200 | 280 | 0,1892 | 4 | |
| Wartungsleistungen | 1.160 | 945 | 215 | 0,1853 | 5 | |
| Schulungsleistungen | 420 | 410 | 10 | 0,0238 | 6 | |
| Gesamt | 8.910 | 3.983 | 4.927 | 0,5530 | ||
| Bereitschaftskosten TEUR | 4.265 | |||||
| Durchschnittlicher Deckungsgrad | 0,5530 | |||||
| Deckungsumsatz TEUR | 7.712 |
Frage: Wie groß ist die Sicherheitsspanne?
Ergebnis: 13,4%
| Umsatz | DB | DB | Gewinn | |
| kum. TEUR | TEUR | kum. TEUR | kum. TEUR | |
| Softwareprodukt A | 2.800 | 2.540 | 2.540 | –1.725 |
| Softwareprodukt B | 4.500 | 1.522 | 4.062 | – 203 |
| Einführungsunterstützung | 5.850 | 360 | 4.422 | 157 |
| Programmierung im Kundenauftrag | 7.330 | 280 | 4.702 | 437 |
| Wartungsleistungen | 8.490 | 215 | 4.917 | 652 |
| Schulungsleistungen | 8.910 | 10 | 4.927 | 662 |
| Gesamt | 4.927 | 4.927 | 662 |
Für die grafische Ermittlung des Deckungsumsatzes im Mehrproduktfall in einem Break-even-Diagramm werden die einzelnen Produkte in der Reihenfolge ihres Deckungsgrades mit ihrem jeweiligen Umsatz und dem dazugehörigen Deckungsbeitrag in ein Koordinatensystem eingetragen. Auf der Abszisse wird der Umsatz abgetragen, auf der Ordinate Deckungsbeitrag und Gewinn. Die kumulierte Gewinnlinie weist wegen des abnehmenden Deckungsgrades der Produkte eine Bogenform auf. Den Deckungsumsatz erhält man, wenn die Verbindungslinie von Ausgangspunkt und Endpunkt der Gewinnlinie gezogen wird. Der Schnittpunkt mit der x-Achse gibt den Deckungsumsatz an.
Eine weitere interessante Variante der Break-even-Analyse stellt die Anwendung auf die Kostendeckung im Zeitablauf dar. Umsatz und Deckungsbeitrag der einzelnen Abrechnungsperioden werden monatlich kumuliert gegenübergestellt. Da das Fixkostenvolumen für das gesamte Jahr in etwa im voraus bestimmt werden kann, lässt sich so bestimmen, bei welchem Umsatzvolumen im Zeitablauf des Jahres die Kostendeckung eintritt.
Literaturhinweis
Kilger/Pampel/Vikas: Flexible Plankostenrechnung und Deckungsbeitragsrechnung, 13. Aufl., 2012.